前言
最近需要完成一个构造数据库的索引的实验,实验要求使用B+树做索引结构,因为对于B+树不够了解,所以先复习一下B+树的特性在进行下一步。对于B+树,这篇文章讲的很好。https://www.cnblogs.com/nullzx/p/8729425.html
B+树结构特点
B+tree是应文件系统所需而产生的一种B树的变形树,一棵m阶的B+树的特点:1.有n棵子树的节点中含有n个关键字。2.所有的叶子节点中包含了全部的关键字信息,及指向含有这些关键字记录的指针,且叶子节点本身依关键字的大小自小到大顺序链接。 3.所有的非叶子节点可以堪称是索引部分,节点中仅含有其子树根结点中最大(或最小)关键字。4.B+树的有效内容均在叶子节点。所有叶子节点中有志向兄弟节点的指针5.B+树的头指针有两个,一个指向根节点,一个指向关键字最小的元素,因此B+树有两种遍历方式。从根节点开始随机查询。从最小关键字顺序查询。
B+树的插入
和其他树形结构一样,B+树也支持插入,删除,遍历等操作。在经过前面两周对B+树的了解后,我认为B+树中最难的应该是元素插入。相对简单的是元素遍历。当然这也是建立在B+树数据结构中具有良好的遍历字段的情况下的。作为同一种数据结构可以不断的修改内部的结构特点,根据实际需要,使得可以方便完成自己的需求。
现在先讲以下B+树的插入:首先假定B+树每一个节点中可以最多可以包含2m个元素,因此对于任意节点来说,不能少于m个元素。对于每一次插入元素,必须遍历b+树的叶子节点,因为叶子中存放的才是有效的元素,在非叶子节点中都是对于叶子节点的索引。这也使得b+树在节点有序的同时,所有叶子节点元素都是有序的。
元素插入分如下情况: 1.节点中元素个数满足m<nodes<2m-1,插入元素后直接返回。 2.节点元素有2m-1个,插入后由于节点满(这里可以根据实际情况决定最多放2m还是2m-1个)。需要进行节点分裂,节点分裂会产生新的节点,同时也会产生新的由父节点指向该节点的索引。此时需要从当前节点向根节点遍历,修改父节点的索引。
- eg1
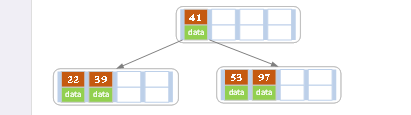
在此时的树中55,则插入元素后直接返回。
- eg2
若在刚才的树中依次插入元素13,21,40,则会造成节点分裂叶子节点分开,同时更新父节点索引,如下图
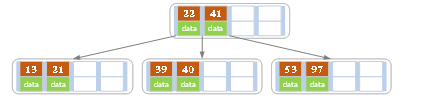
如果不断插入元素导致非叶子节点也到达满的情况。按照叶子节点的分裂情况处理即可。
B+树的删除
B+树的删除就相对来说比较困难了,如果删除元素后节点数满足m<nodes<2m,则可以直接返回,否则需要进行修改。
B+树的删除分如下情况。 1.删除后节点元素个数满足m<nodes<2m,直接返回。但是如果删除的式节点中的第一个元素,则需要视情况更新索引。 2.删除后节点元素小于m,则考虑向左边或者右边借一个元素进行合并。 3.在2的条件下,左边叶子节点元素个数满足条件,则分一个给右边节点,同时因为元素的有序性,分给右边的元素占据第一个,所以需要更新当前节点索引。 4.在2的情况下,如果左节点不满足,则向右边节点借一个,如果右边节点满足,分出一个元素,同时需要更新右边节点的索引。 5. 如果3 4都不满足,则需要进行节点合并,与哪边合并都可以,此时需要删除父节点的一个索引。
总体来看,删除操作略微复杂。
- eg1
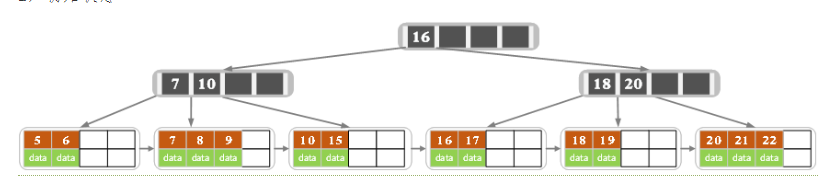
此时删除元素22后,可以直接返回
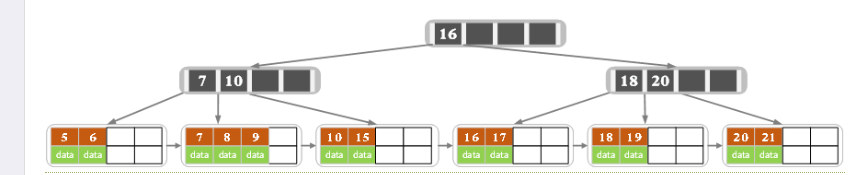
- eg2
删除22后,删除15,结果如下。
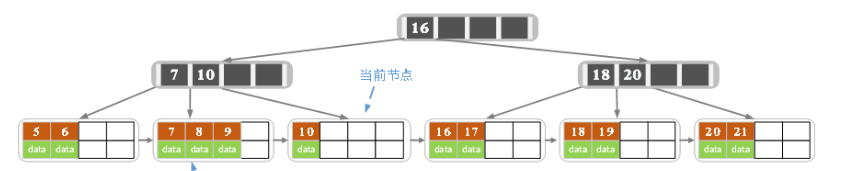
此时需要借元素,同时更新索引
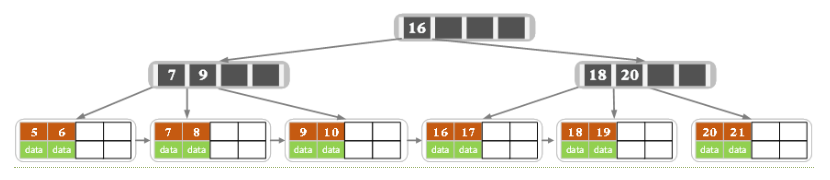
- eg3
现在删除元素7,则需要进行节点合并,由于删除的7式一个索引,则也需要更新索引。
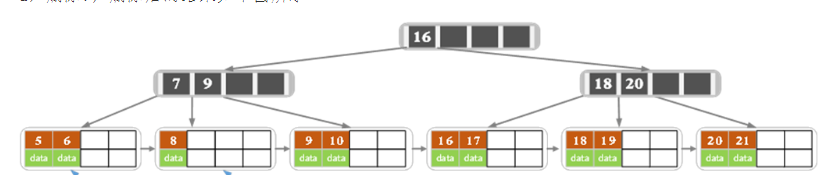
合并后如下:
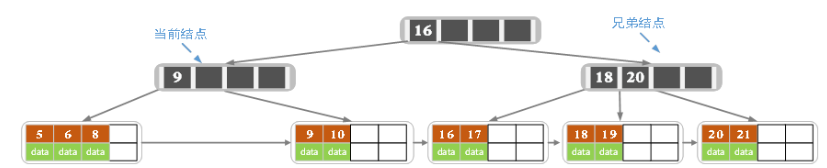
由于更新后的父节点只有一个索引不满足条件,则该节点也需要合并,最后如下

B+树的遍历
B+树可以分两种遍历方式,可以从根节点进行遍历,页可以根据需要,适当修改节点数据结构,直接从最左边叶子节点遍历,两种情况都比较简单,第一种是O(logn)的复杂度,第二种是O(n)的复杂度。
总结
B+树整体操作如上述,当遇到问题时,其实一种数据结构有时候并不是那么高深莫测,它只是通过某些变形而已,需要结合实际情况,考虑所学的基本知识进行变通。尤其是对基础知识牢固把握时很重要的。并没有很难得知识点,都是通过基础一点点得变化而来。