前言
发现之前对于散列表这个数据结构一直有点模糊不清,今天手上正好带了算法这本书,就系统的过一遍,加深下印象。
散列表特性
散列表作为一种动态的结构,其空间是随着数据的插入和删除不断变化的,他也是数组概念的扩展,在支持insert,delete,search的操作的同时能够进一步降低时间复杂度。在设计合理的情况下,上述操作的复杂度能够降到o(1)。散列表的特性是1.实际存储的关键字数目比关键字总数小。2.通过计算得到关键字的下标。对应的方式是hash中解决冲突的策略。
直接寻址表
当关键字的域范围比较小时,可以使用直接寻址,使用一个数组作为直接寻址表,表中每一个位置称为slot(槽),每个slot存放一个关键字。没有存放关键字的slot用特殊值代替。 优点是效率很高,缺点是条件很苛刻,属于比较理想的情况。对于空间的浪费比较严重。
散列表
在直接寻址方式中对于空间的浪费比较严重,所以考虑将关键字的域通过一个函数计算进行放缩,这个函数称为hash函数,h:U→{0,1,2,…m-1};
通过这样一个函数对关键字进行计算将U范围的数据放缩到m的空间大小中,节约了很多空间,但是也带来了一个问题,可能有多个关键字会映射到一个slot上,称为冲突,不过有很多的办法来解决冲突。
链地址法
链地址的存放方式如下:
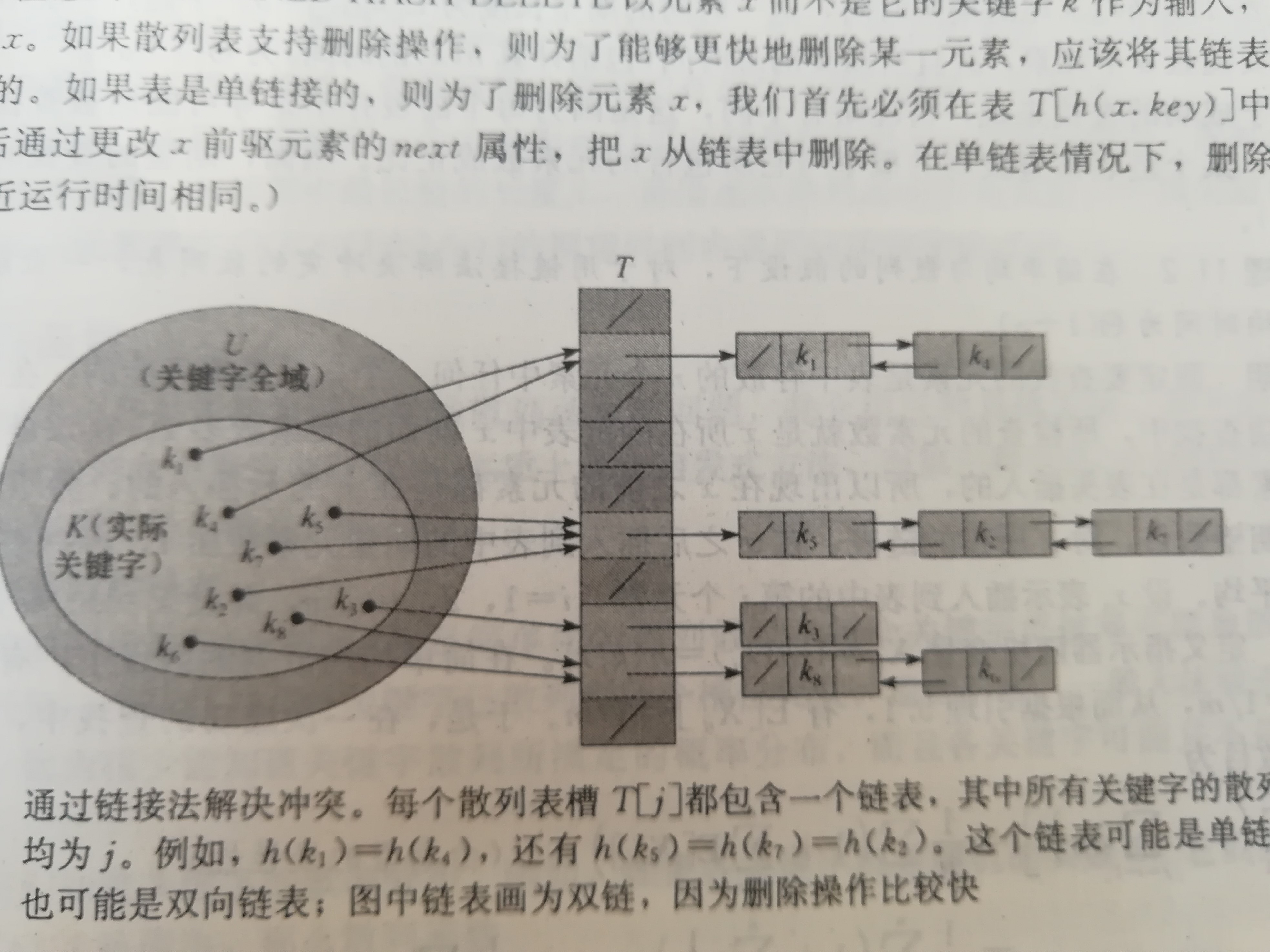
其中的链表可以采用单链表或者双向链表,在同一个链表中关键字的hash值是相同的。
性能分析:定义装载因子为a=n/m,(n表示关键字个数,m表示散列表大小),因此当m与n成正比时(a<1)可以实现在o(1)的时间内进行查找,删除,和插入元素。
散列函数
在设计散列函数时需要近似的满足简单均匀散列假设:每个关键字等可能的散列到槽位的任何一个。
设计方法:1. 利用关键字分布的有用信息,尽量降低将相似符号散列到相同位置。2.一个好的方法导出的散列值应该可以独立数据可能存在的任何模式。3.让近似的关键字具有截然不同的散列值。
除法散列法
h(k)=kmodm;
散列法设计的好坏关系到散列表的冲突大小,使用除法散列时尽量避免m为2的幂,可以选择接近2的幂的一个质数作为m.
乘法散列法
乘法散列法的设计步骤1.用关键字k乘上常数A(0<A<1),提取kA的小数部分,步骤2.用m乘以这个数在向下取整 h(k)=m(kA mode 1);
寻址方式–开放寻址法
在开放寻址法中,所有元素都存放在散列表中,也就是说,每一个表项或包含一个元素或者为空。当查找某个元素时,要系统的检查所有表项,直到找到所需的元素或者最终发现元素不在表中。这里面没有链表,元素都存放在散列表外,因此在开放寻址法中a不能超过1.
开放寻址法–线性探测
给定一个普通函数作为散列函数,h(k,i)=(h`(k)+i) mod m; i=0,1,2…m-1; 给定一个关键字k,根据 h’(k)获得一个槽位,如果发生冲突,则使用上述公式推进到下一个位置。 极端情况是遍历了整个散列表。 因此存在的问题称为一次群集,随着占用槽位的不断增加,平均查找时间也会不断增加。
开放寻址法–二次探测
二次探测使用函数如下 h(k,i)=(h`(k)+c1i+c2i^2)mod m;i=0,1,2…m-1; 这个方式需要探查的槽位会比线性探测的方式少。但是也会出现二次群集的问题。
开放寻址法–双重散列
双重散列是对上述两种方式的优化, hash函数为 h(k,i)=(h1(k)+i*h2(k))mod m; 这种方式使得关键字以两种不同的方式依赖于hash函数,因此效果是比较理想的,但是在设计时为了遍历到整个散列表需要确保h2(k)与m互素。因为这样的数据相对密度可能较小。