前言
本着复习的理念,还是简单梳理一遍常见的排序算法,直接贴出代码,并且在代码中加以注释。
排序算法对比
说到排序算法,那还是就放这张图就可以了。
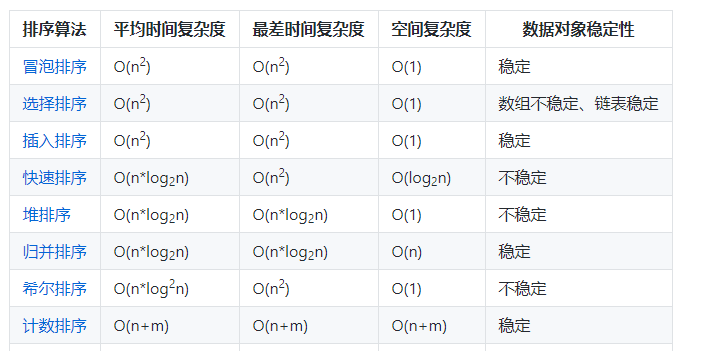
本文实现了上述的几种算法,上面没提到的桶排序和基数排序并没有加以实现。
稳定性
稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
运行结果如下:
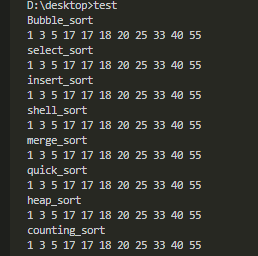
#include<vector>
#include<iostream>
#include<string.h>
using namespace std;
/*冒泡排序 时间复杂度 O(n^2);
可以修改其中的条件使其稳定或者不稳定
主要思路就是通过不断比较相邻的数据大小,并进行交换。
如果数据原本就是有序的,那么无需交换,但是循环次数不变
*/
void Bubble_sort(vector<int>& temp){
int size = temp.size();
for (int i = 0; i < size-1;i++){
for (int j = 1; j < size;j++){
if(temp[j-1]>temp[j])
swap(temp[j-1], temp[j]);
}
}
return;
}
//select sort
/*选择排序 O(n^2)
选择排序的思路也比较简单,多次循环数组,每次找到当前循环的最小值,记录下标,每次找到最小值后放到(swap)前面已排好序的末尾即可。
如果数组全都排好序,那就不必交换,但是循环次数不变。
*/
void select_sort(vector<int>& tmp){
int size = tmp.size();
for (int i = 0; i < size-1;i++){
int minindex = i;
for (int j = i+1; j < size;j++){
if(tmp[j]<tmp[minindex])
minindex = j;
}
swap(tmp[minindex], tmp[i]);
}
return;
}
/*插入排序 O(n^2)
我习惯将插入排序和选择排序做比较,当然两者的思路都比较直接,每次从当前位置向前看,比前面的元素小就交换,否则继续下一次循环,因为每次向后推进前面的 元素都是已经排好序的。
因此最好情况为O(n)
*/
void insert_sort(vector<int> & tmp){
int size = tmp.size();
for (int i = 0; i < size - 1;i++){
for (int j = i + 1; j >0;j--){
if(tmp[j-1]>tmp[j])
swap(tmp[j - 1], tmp[j]);
else break;
}
}
return;
}
/*希尔排序:思路不够直接,
主要是先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序。复杂度O(n^2);最好为o(n);
*/
void shellsort(vector<int>& tmp){
int size = tmp.size();
for (int gap = (size / 2); gap > 0;gap=gap/2){
for (int i = gap; i < size; i++)
{
int j = i;
int cur = tmp[i];
while((j-gap)>=0 && cur<tmp[j-gap]){
tmp[j] = tmp[j - gap];
j = j - gap;
}
tmp[j] = cur;
}
}
return;
}
//quick_sort 复杂度O(nlogn),如果数组原本有序,那么就会变为O(n^2),个人认为退化为冒泡了;
/*算法思想的典型使用,选取一个flag,从左右开始,小于flag就将交换left和right元素,同时left右移,大于flag也交换位置,同时right左移。
当循环结束后将flag放回到left==right的位置
分别对左部和右部进行相同的排序,递归出口为right-left<=0
*/
void quick_sort(vector<int>& tmp,int left,int right){
if(left>=right)
return;
int flag = tmp[left];
int tmpl=left;
int tmpr = right;
while(tmpl<tmpr){
while( tmpr>tmpl && tmp[tmpr]>=flag)
tmpr--;
if(tmpr>tmpl)
tmp[tmpl] = tmp[tmpr];
while(tmpl<tmpr && tmp[tmpl]<flag)
tmpl++;
if(tmpr>tmpl)
tmp[tmpr] = tmp[tmpl];
}
//完成一遍后把flag放回tmp
tmp[tmpl] = flag;
quick_sort(tmp, left, tmpl);
quick_sort(tmp, tmpr + 1, right);
}
//heap sort makeheap popheap sortheap
// O(nlogn)
/*三个步骤,make_heap:将最大元素放在堆(数组)首部
pop_heap:取出最大元素放到heap(数组)尾部同时缩小堆范围
sort_heap:循坏执行make和pop操作,逐渐减小堆。最后得到有序数组
*/
void makeheap(vector<int>&tmp,int pare,int curlen){
int cur = tmp[pare];
int child = pare * 2 + 1; //左孩子
while(child<curlen){
if(child+1<curlen && tmp[child+1]>tmp[child]){
child++;
}
if(tmp[child]>tmp[pare]){
swap(tmp[child], tmp[pare]);
pare = child;
child=child*2+1;
}else break;
} //o(logn)
}
void popheap(vector<int>& tmp,int index){
swap(tmp[0], tmp[index]);
}
void heapsort(vector<int> & tmp){
int size = tmp.size();
int child = size / 2 - 1; //确保第一个节点有孩子
for (int i = child; i >= 0;i--)
makeheap(tmp, i, size);
for (int i = size - 1; i > 0; i--){
popheap(tmp,i);
makeheap(tmp, 0, i);
}
}
///count_sort
/* 复杂度为o(n);
一边用来数组差别不大的排序中,统计字符串中字母个数时也可以用到这个方法
*/
void counting_sort(vector<int>&tmp){
int min=65535,max=-65535;
int size = tmp.size();
for (int i = 0; i < size;i++){
if(tmp[i]<min)
min = tmp[i];
if(tmp[i]>max)
max = tmp[i];
}
int flag[max - min + 1];
memset(flag, 0, sizeof(flag));
for (int i = 0; i < size;i++){
flag[tmp[i] - min]++;
}
int index = 0;
for (int i = 0; i < max - min + 1;i++)
while(flag[i]>0){
tmp[index++] = i + min;
flag[i]--;
}
}
/*归并排序:将数组分为各个部分排好序后再合并
复杂度为O(nlogn)
*/
void merge(vector<int>&tmp,int lefthelp,int mid,int right){
int left = lefthelp;
vector<int> help(right - left+1,0); //注意此处需要保证左右的空间,因此尽量让right指向back而不是end
int k = 0;
int index = mid + 1;
while(left<=mid &&index<=right){
if(tmp[left]>tmp[index]){
help[k++] = tmp[index];
index++;
}else{
help[k++] = tmp[left];
left++;
}
}
//出现多余一个的情况
while(left<=mid)
help[k++] = tmp[left++];
while(index<=right)
help[k++] = tmp[index++];
for (int i = 0; i <= (right - lefthelp);i++)
tmp[i + lefthelp] = help[i];
}
void merge_sort(vector<int>&tmp,int left,int right){
if(left<right){
int mid = (left + right) / 2;
merge_sort(tmp, left, mid);
merge_sort(tmp, mid + 1, right);
merge(tmp,left,mid,right);
}
}
void print(const vector<int> tmp){
for (int i = 0; i < tmp.size();i++)
cout << tmp[i] << " ";
cout << endl;
}
int main(){
vector<int> test = {3,1, 40, 5, 18, 25, 33, 17, 17, 20,55};
//1.bubblesort
vector<int> tmp = test;
cout << "Bubble_sort" << endl;
Bubble_sort(tmp);
print(tmp);
// for (int i = 0; i < tmp.capacity();i++)
// cout << &tmp[i] << " ";
// //2.selectsort
// cout << endl;
tmp = test;
// for (int i = 0; i < tmp.capacity(); i++)
// cout << &tmp[i] << " ";
// print(tmp);
cout << "select_sort" << endl;
select_sort(tmp);
print(tmp);
//3.insert_sort
cout << "insert_sort" << endl;
tmp = test;
insert_sort(tmp);
print(tmp);
//4.shell sort
tmp = test;
cout << "shell_sort" << endl;
shellsort(tmp);
print(tmp);
//5.merge_sort
tmp = test;
cout << "merge_sort" << endl;
merge_sort(tmp, 0, tmp.size()-1);
print(tmp);
//6.quick sort
tmp = test;
cout << "quick_sort" << endl;
quick_sort(tmp, 0, tmp.size() - 1);
print(tmp);
//7.heap_sort
tmp = test;
cout << "heap_sort" << endl;
heap_sort(tmp, tmp.size() - 1);
print(tmp);
//count_sort
tmp = test;
cout << "counting_sort" << endl;
counting_sort(tmp);
print(tmp);
return 0;
}; note 8.28补充
我突然想到一个关于=的问题,上述的vector赋值我都是使用=进行赋值的,那么=对于很多类来说都是一个浅拷贝,当然如果vector自身已经重写了拷贝构造函数的话那就是一个深拷贝了。
想到问题后,我找了一些资料,没有找到相应的源码,但是找到一篇关于这部分知识的博文,感觉还行。https://blog.csdn.net/vict_wang/article/details/88812389,这来看,在vector中使用a=b,a(b)也都是深拷贝了,当然还有上述博客中的assign 和swap也是深拷贝模式,我也实践了一下,在源码中打印他们的地址,发现最后证明确实是深拷贝。所以上述的排序源码应该没问题吧。