前言
此次复习主要参考侯捷翻译的《STL源码剖析》之前一段时间已经看过一遍STL,但是有些东西总是会忘记,为了加深记忆,也为了之后秋招着想,最近一天再将这本书过一遍,相信再看第二遍的时候一定会有不一样的收获,之前没有看的时候没有加入任何笔记,好在这次可以记录在博客里,一些我认为已经不必要或者我已经记的很清楚的东西将不再重复。我会按照章节来进行复习。当然,这本书也包括了c++和c中各方面的知识,我所能做的就是尽量理解透彻当前我所知道的那部分。有些东西还是需要慢慢积累的。
第一章 STL概论于版本简介
STL六大组件
1.容器 指STL中的各种数据结构,比如 vector list deque map set等,这些容器中已经封装了各种各样的算法,从实现的角度看属于一种类模板(class template)
2.算法 算法中包括了很多STL中常用的一些,比如 sort search copy等,从实现的角度看STL算法是函数模板(function template)还有一些很简单的算法,但是其实现机制也是相当简单,大致就是你觉得这个算法你也可以实现,而且你的方法也很简单了,但是这个算法的源码却是更加简单,可以这么说——他想尽一切办法来减少内存和提升速度。
3.迭代器 迭代器是连接在算法和容器之间的桥梁,是一种泛型指针,在STL迭代器是重载了 *operator operator-> operator++ operator– **等相关操作的 class template,类比之后,原生指针(int * 等)也是一种迭代器,迭代器也是一种智能指针。
4.仿函数 行为类似函数,可作为算法的某种策略,这个当时我也没太关注,之后需要好好注意一下。
5.配接器 是一种用来修饰容器或者仿函数,迭代器的东西,比如stack和queue,priority_queue,虽然表面看是一种容器,但是底层完全是依靠deque的结构特性来实现的。
6.配置器 主要是完成STL内存空间的管理和配置。
GNU源码开放精神
STL的实现版本有多种,但是全世界所有的STL的实现版本都源于 Alexander Stepanov和 Meng Lee完成的原始版本,每一个头文件都有一个声明,这份原始版本由惠普公司拥有,允许任何人任意运用,修改,拷贝传播,贩卖这些代码,唯一条件是将这份声明加入新开发的文件内。
STL的版本由很多,有兴趣的可以去找一下,本书使用的是SGI STL这个版本。
STL中一些c++语法
- 静态常量数据成员在类内部直接初试化。
- 迭代器的++/– 因为STL中各种容器需要根据自身的特性完成迭代器的移动,所以,不同的容器会对迭代器进行不同的运算符重载。
- [ )表示法,这一点是我认为比较重要的,这一点直接表示了在STL中 back和end的区别,在STL中所有区间都是一个前闭后开的区间,因此end一般指最后一个元素的下一位置,而back刚好指向最后一个元素,同样的思维可以和erase算法比较
(现在记不太清)。
第二章 空间配置器
空间配置这部分其实在使用STL时都会很少注意到,但是这也是使得STL可以完美运行的底层必要的东西。
说到空间配置就需要提allocator(内存配置器),下面列出STL中allocator的一些接口,可以从命名中看出这些接口的特性。
- allocator::value_type
- allocator::pointer
- allocator::const_pointer
- allocator::reference
- allocator::const_reference
- allocator::size_type
- allocator::difference_type
- allocator::rebind
值得注意的是SGI配置并不是上述的allocator,其名称是alloc,而且其中缺省的就是使用alloc配置器这一点是与其他版本STL不同之一,至于理由就是认为allocator效率不如alloc,allcator只是将c++中的new和delete做了一层简单的封装而已。
一般来讲,我们习惯的内存配置是这样的,
class A{};
A* tmp=new A;
delete tmp;这其中的顺序是,new分配内存,然后构造类对象,删除时则是先调用析构函数将对象析构,然后使用delete释放空间。在STL allocator中这两步分开由 内存配置alloc::allocate()和内存释放由alloc::deallocate()完成。对象构造由::construct()完成,对象析构由::destroy()完成。
空间的配置与释放
前面已经说过,对象构造前的空间配置和对象析构后的空间释放由alloc完成,其设计如下:
- 向system heap(堆)申请内存
- 考虑多线程状态(不太明白,本书没讲)
- 考虑内存不足时的应变措施
- 考虑过多小型区块造成的内存碎片问题。
c++和c的内存分配分别是 new/malloc ,释放则是 delete/free,而在SGI STL中设计了双层的空间配置器,第一级使用malloc和free,第二级则采用如下策略:
当配置区块超过128bytes时,认为空间足够大,使用第一级配置
器,当小于128bytes时,认为过小,使用memory pool处理方式,不再使用第一级配置器。
STL空间配置第一级配置以malloc,free,relloc来执行,不是直接运用C++ new-handler机制(new-handler机制是:要求系统在内存配置需求无法被满足时,调用一个你所指定的函数,在此处大意为,在new无法满足内存需求,抛出bad_alloc之前,会先调,用客户端指定的函数)
按上述的话,当第一级空间配置无法满足或者分配空间小于128bytes时,就会调用第二级空间配置器。第二级空间配置的做法是以内存池管理,每次配置一大块内存,并维护对应的自由链表(free-list),下次如果有相同大小的需求,直接从free-list中拨出,如果客户端释放小额区块,就有配置器返还到free-list中。free-list维护16个节点,每个节点各自管理8,16,24,32,40,48,56,64,72,80,88,96,104,112,120,128bytes的大小空间。如果free-list中也没有可用区块,需要调用refill()进行填充,其新取得的空间来自内存池,缺省为20个节点,也可能小于20个。如果内存池中也无法取得足够的空间,同时堆中的空间也不足,那将无法解决申请空间的问题,
第三章 迭代器概念与traits编程技法
iterator模式定义如下:提供一种方法,使之能够依序寻访某个容器的各个元素,而又无需暴露出容器的表述方式。
iteartor是一种smart pointer。关于smart pointer可以参考其他博客,不过之后我也会复习到。大概就是智能指针也是一个类,极大的帮助编写人员减小内存泄漏的问题。
模板偏特化的意义
如果class template 拥有两个或以上的参数,我们可以对其中某个但不是全部的template参数进行偏特化,换句话说,我们可以在泛化设计中提供一个特化版本。
根据经验,最常用到的迭代器类型有五种, value type,difference type, pointer,reference,iterator catagory
- value type指的是迭代器所指对象的型别,任何一个class中用到了 STL,就需要定义自己的value type。
- difference type表示两个迭代器之间的距离,因此也可表示容器的最大容量。
- iterator_catagory根据不同容器的移动特性和操作,分为下面几类
input iterator:迭代器所指对象只读
output iterator:迭代器所指对象只写
forward iterator:可以向前移动,且可读可写
bidirectional iterator:可双向移动,
random iterator: 具有算术能力,可以随机访问比如vector的迭代器
第四章 序列式容器
stl中各种容器关系如下:
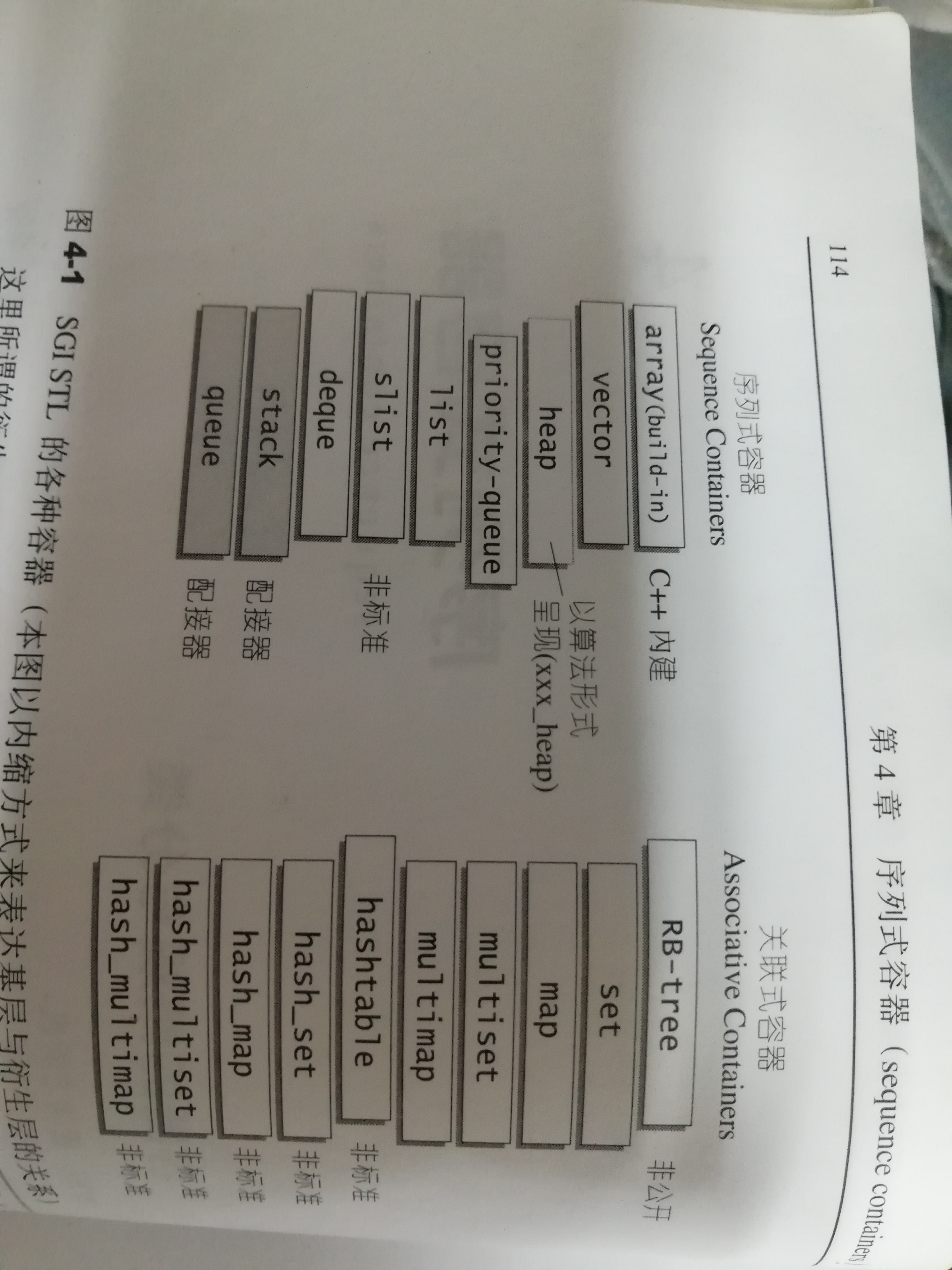
序列式容器指容器中元素都可序但未必是有序的。比如 array,vector,list deque。
vector
note:8.22更新
由于array不属于STL的一部分,在此就不过多讲述,但是vector和array是比较相似的,差别在于array是静态的空间,一旦配置了大小就不能在改变,而vector比较灵活。空间配置是一个较大耗费时间的工程,分为(配置新空间,数据移动,释放旧空间)。所以在vector中增加空间时一般都是按照当前空间大小的两倍来增加。
vector迭代器
根据vector的性质,其维护的是一段连续空间,需要能够访问其中任意一个元素,按前面迭代器的类型可知使用的是random iterator,可以进行算术运算。
vector数据结构
大致形式如下:
class vector{
...
protected:
iterator start; //当前使用空间头部
iterator finish;//当前使用空间尾部
iterator end_of_storage; //当前可用空间尾部
...
}所以vector的容量(capacity)永远大于或等于其大小。如果容量等于大小,当扩充大小时就需要—配置新空间,数据移动,释放旧空间。将空间扩展为当前的两倍,然后移动数据,释放原空间,如果两倍不够,则获取更大的空间。
vector 元素操作
vector元素操作很多,这里整理其中一部分,
首先区别
capacity()//大于等于size()
size() //当前元素的个数pop_back()
{
--finish;//finish指向最后元素的下一位置
destroy(finish); //释放空间
}erase()
//删除范围内所有元素
iterator erase(iterator first, iterator last)
{
iterator i= copy(last,finish,first);
destroy(i,finish); //析构对象,空间仍可用
finish= finish-(last-first);
return first;
}
//删除指定元素
iterator erase(iterator pos){
if((pos+1)!=end()) //不是最后一个元素,吧后面的元素向前移动
copy(pos+1,finish,pos);
--finish;
destroy(finish);
return pos;//返回删除元素的后一个元素
}insert(postion,n,x)//在postion插入n个x元素,返回position
需要注意的一点是STL的规范插入节点应该在所指position(节点)的前方。
clear(),清空所有对象,但是空间任然可用。
list
概述
顾名思义,list就是链表,不过STL的list是双向链表,且其中有list迭代器,结合链表的特性,删除和插入元素都是常数时间复杂度。
list节点:
template<class T>
struct _list_node{
typedef void* pointer;
void_pointer pre;
void_pointer next;
T data;
}从节点设计也可以看出是双向链表,考虑其迭代器,需要访问其中的任意数据,但是空间不是连续的,所以无法进行算术运算,由于本质是双向链表,所以能前后移动,使用bidirectional iterator。由于地址空间不是连续的,所以插入和删除操作不会造成后续的迭代器失效,删除操作也只会造成被删除的那个迭代器失效,这是list的一个特征。
更特别的是SGI STL的list是双向循环链表,为了表示前闭后开区间,最后一个元素的数据域为空,而且只需要一个iterator就可以遍历整个list。
list 元素操作
下面简述部分list中的操作
//插入一个头节点
void push_front(const T&x){
insert(begin(),x);//insert的一种重载方式
}
//插入一个尾节点
void push_back(const T&x){
insert(end(),x);//end()是最后一个元素下一个位置
}
//移出迭代器所指节点
iterator erase(iterator pos){
....
//于链表操作一致
return iterator(next_pos);//返回下一个节点
}
void pop_front()//移出头节点
void pop_back()//移出尾节点
void list<T,Alloc> ::remove(const T& x);//移出值为x的节点
void list<T,Alloc>:: unique();//移出连续且相同元素中多个,只留下一个
void list<T,Alloc>:: reverse();//数据翻转
void list<T,Alloc>::sort();// STL 算法提供的sort必须传入随机访问迭代器 ,这是list自己的sortdeque
和vector做对比,vector是单向开口的连续序列,deque是双向开口的连续序列。的却相较于vector的最大优点就是可以常数时间内在头部进行插入。而且deque没有容量的概念,他是动态的以分段连续的空间组合起来的。原书中如下讲述:** 虽然deque也提供random access iterator,但是他的迭代器比较复杂,如非必要,尽量使用vector代替deque,deque的sort操作,为了提高效率,是先复制到vector中再排序,然后复制回deque中。
deque构造
deque采用连续分段的map(不是STL中的map)作为主控,每个map中的节点指向一块连续的线性空间,该空间才是deque主要存储区。
结构如下:
template<class T,Alloc=alloc,size_t BufSize=0>
class deque{
public:
typedef T value_type;
typedef value_typ* pointer;
…
protected:
typedef pointer map_pointer;
map_pointer map; //指向连续空间,其中每个空间都是一个指向缓冲区的指针
size_type map_size; //map内可容纳的指针
}
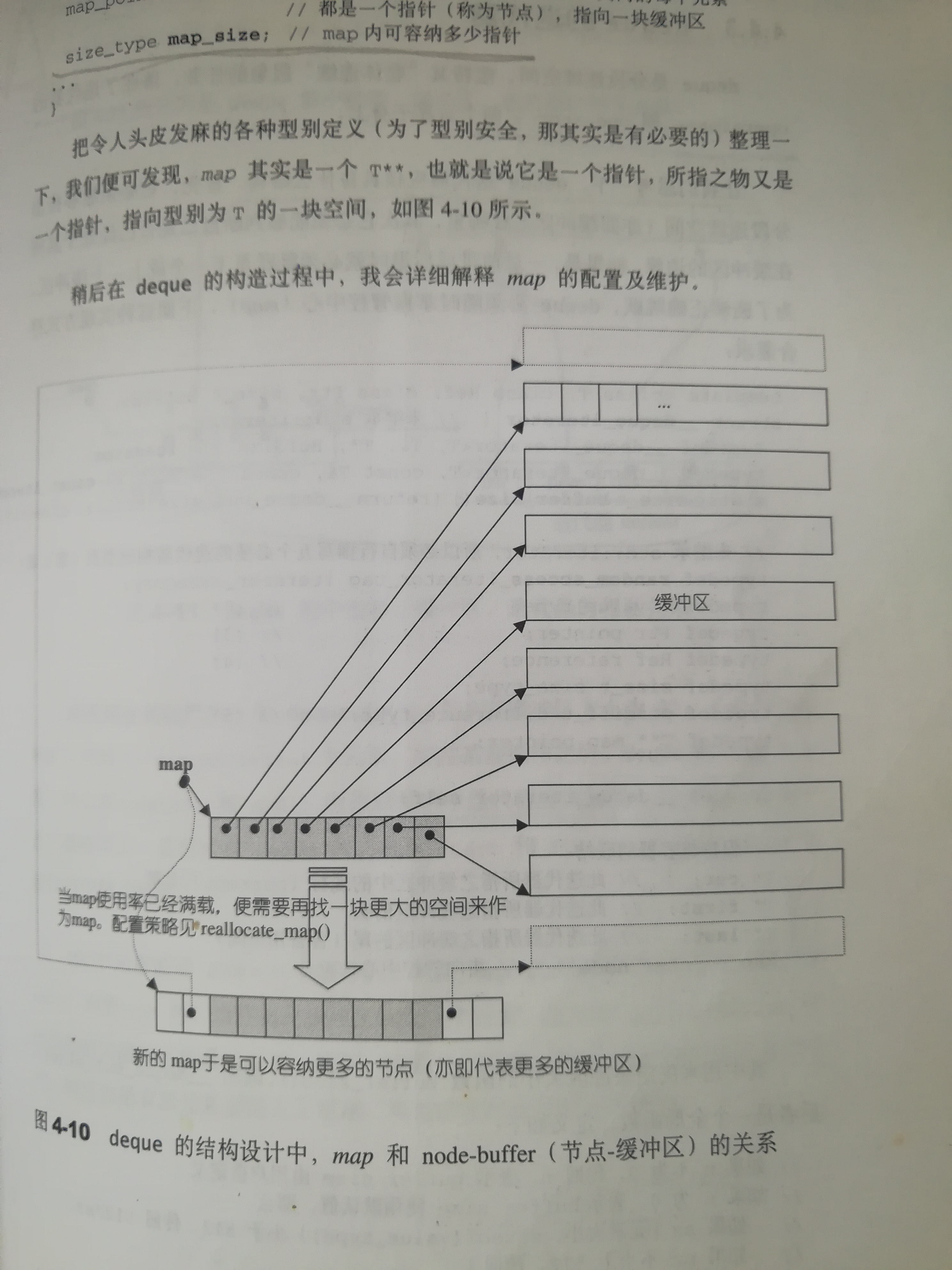
deque迭代器
为了维持“整体连续”,deque的迭代器需要实现operator–和operator++的功能,结合deque的结构,为了保证一个缓冲区满后可以跳到相邻的另一个缓冲区,必须管理好其中的map
deque元素操作
deque可以使用随机访问迭代器,注意其和vector的差别在于表面上是连续存储,可以双端插入数据
| 方法 | 含义 |
|---|
stack
stack是一种后进先出的数据结构,只有一端开口,在本书中,采用deque作为底层的结构,构造stack,也可以使用list构造stack,list和deque一样都是两端开口的,只要保证使用时指开启一段即可。
主要元素操作:
push()//向stack中推入一个元素
pop()//取出栈顶元素
top() //获取栈顶元素
size() //获取元素个数
empty() //判断栈空queue
queue是一种先进先出的数据结构有两个开口,结合前面说述,SGI STL底层使用deque是西安queue,可以说完成了queue的所有性能,与stack相同,queue也没有迭代器,只能从一段进,另一端出。支持的元素操作
push()//向queue中推入一个元素
pop()//取出栈顶元素
front() //获取栈顶元素
size() //获取元素个数
empty() //判断栈空
back() //获取尾端元素heap概述
heap并不是stl中的容器或者配接器,但是他是是西安priority_queue(优先)的助手,优先队列是指队列首部元素永远是其中的极值元素。要实现优先队列需要实现堆算法
heap算法
堆分为max heap 和min heap,下面以maxheap为例,整个堆算法包裹 push_heap pop_heap sort_heap
pushheap:
push_heap所形成的是完全二叉树,要实现大顶堆,每次新加入的元素都是在最下一层的叶节点,新元素是否属于这个位置(每个节点的值都大于或者等于子节点的值),每次加入一个新节点就进行上溯,与其父节点比较,大就对换位置,直到不能换位置即可。注意任意节点(i)的父节点可表示(i((i-1)/2).
popheap:
前面实现的大顶堆只有根节点是最大的,要保证每次取出一个节点后剩余节点最大值也在根节点,需要进行popheap,具体做法是:**每次循环取出一个最大元素后,将其和末尾元素(最后一个叶子节点交换),同时堆的大小减1,此时将堆进行调整,比较其和子节点大小,并交换其位置,直到对末尾。(注意此时堆的大小已经变化)。整个完成后便从小到大排好了序。
sortheap:
按前面所述,只要完成了pushheap popheap,每次减小堆大小最后就可以实现堆排序。
heap不提供迭代器,但是可以使用algorithm中实现的堆算法进行排序
make_heap() //构造一个大顶堆
push_heap() //向堆中加入元素,同时保证大顶堆的特性
pop_heap() //从堆中取出一个元素,同时保证大顶堆的特性
sort_heap() //进行堆排序priority_queue
优先队列,有heap构成,没有迭代器,处于最顶端的元素是最大值或者最小值,缺省使用vector作为底层容器。
支持的部分元素操作:
empty() //是否为空
size() //大小
top() //获取首部元素
push() //向尾部插入元素,且保证队列的优先特性
pop() //取出末尾元素,slist
STL list 是一个双向链表,slist是单项链表,考虑到器结构特性,只能向后遍历数据,因此其迭代器的类型是forward iterator,指向slit的首节点,因此slist一般只适合在头部进行元素的插入。所以插入的元素顺序会和slist表现出来的顺序相反。
slist元素操作与我们构造的链表操作差别不大,其中表头是一个不含元素的空节点,这样方便在head部分插入元素。
元素操作:
push_front() //头部插入元素
size() //元素个数
find() //查找某个元素
insert() //插入元素第六章 关联式容器
关联式容器分为set和map两大类,以及衍生出的multiset,multimap,这些容器底层均以红黑树完成。 红黑树也是一个独立容器,但不开放给外界使用
SGI STL还提供了一个不再标准规格内的关联式容器,hashtable, 以及以hashtable为底层的hashmap和hashset hash_multiset, hash_multimap
关联式容器类似关联数据库,每一笔数据都有一个key和value,内部以找key的值放于适当位置,因此没有头和尾部,也就没有 push_back(),push_front() pop_back() 等元素操作。
树的导览
二叉搜索树
是指可提供对数时间的元素插入和访问,二叉搜索树的防止规则是:任何节点的键值一定大于左孩子的键值且小于右孩子的键值。因此一致往左走,走到最后可得到最小值,一直往右走,走到最后可得到最大值。
平衡二叉搜索树(AVL树)
平衡二叉树:它是一棵空树或者左右两个子树的高度差的绝对值不超过1,并且左右子树都是一棵平衡二叉树。
AVL树: 树的每个左子树和右子树都是AVL树
左子树与右子树高度之差的绝对值不超过1
每一个节点都有一个平衡因子(balance factor),任一节点的平衡因子是-1、0、1(每一个节点的平衡因子 = 右子树高度 - 左子树高度)
当插入新的节点后可能会破坏原有树的平衡性,需要进行调整,即进行节点旋转。
红黑树
是一个二叉搜索树,且满足1.每个节点不是红色就是黑色,2.根节点为黑色
3.如果节点为红色,那么其子节点为黑色.4.任一个节点至NULL的任何路径所包含的黑色节点数相同。
2019.9.6补充
相比于AVL,红黑树不是严格平衡的,在多次插入元素后,AVL树的效率编得低下,当AVL删除元素时,需要维护这条路径上被影响的所有节点,复杂度为O(logn).而RB树每次插入/删除元素只需最多三次旋转。
RBtree 迭代器
RBtree迭代其属于双向迭代器,但不具备随机定位的能力,因此其迭代器的类型应该是bidirectional iterator
RBtree元素操作
RBtree提供两种元素操作, insert_unique(),insert_equal();
insert_equal()
插入新值,节点键值允许重复。
insert_unique()
插入新值,节点键值不允许重复,返回一个pair,第一个元素是RBtree的迭代器,第二个元素表示插入成功与否。
在RBtree中每次插入元素后都需要进行调整,保证树的状态符合RBtree的要求。
set
set的特性是只有一个键值,且键值就是实值。set不允许右两个元素相同的键值。不可以通过set的迭代器改变set的元素值。元素值关系到set的排序规则。 因此set的迭代器是一种 constant iterator(只读)。set和list有相同之处。在增加或者删除元素后,其余迭代器都是有效的。
由于底层是RBtree,所以有很好的排序效果。
int main(){
set<int> test;
test.insert(5);
test.insert(7);
test.insert(2);
test.insert(-1);
test.insert(18);
test.insert(6);
test.insert(1);
test.insert(15);
for (auto it = test.begin(); it != test.end();it++)
cout << *it << " ";
return 0;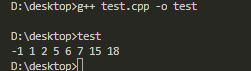
其中元素已经自动排好序了。
由于map和set性质类似,元素操作也类似,放在后面一起讲述
map
map特性是根据元素键值自动排序,map所有元素都是pair,同时拥有key和value,可以通过pair访问每一个元素的key和value同时不可以通过map迭代器修改map的元素内容,因此内部迭代器也是 constant iterator(只读)
元素操作如下:
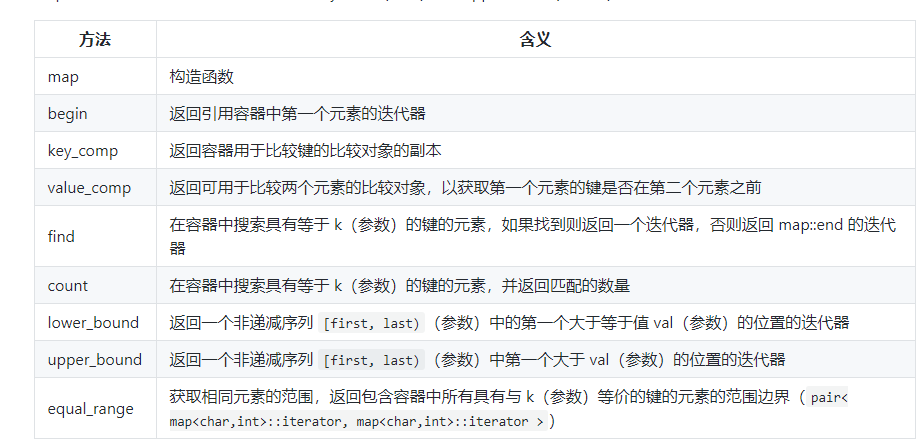
同时也有如下操作:
size() //返回元素个数
empty() //是否为空
operator[]() //map独有 可以访问key和valuemultiset和multimap结构与上述完全一致,只是其中可以插入相同的元素。在此不再赘述。
hashtable
hashtable优点在于在插入,删除,查找等方面也有常数的平均时间复杂度。不过其底层是通过hash算法实现的,底层hashmap和hashset的操作也map set类似,综合总结如下:
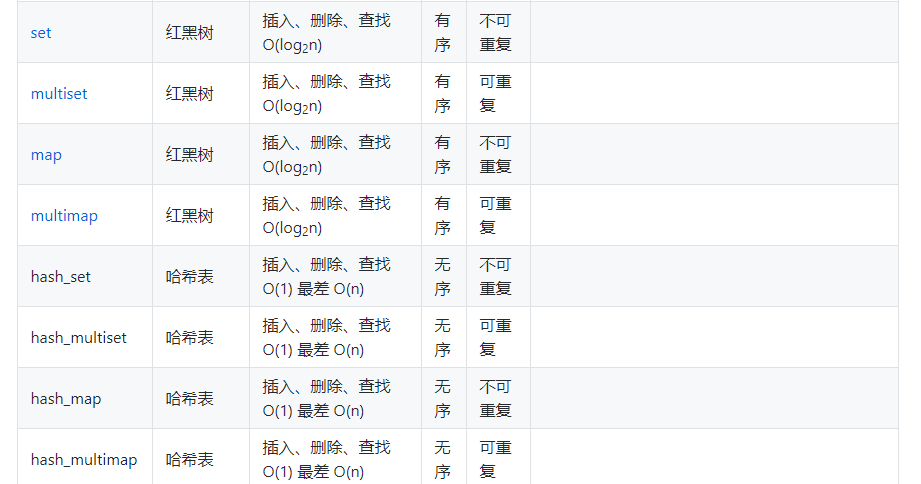
其元素操作也与上述map,set类似,不再赘述。需要注意的是以hashtable为底层机制实现的容器,其元素并未有序。
Note: 2019.9.10更新
TreeMap是基于树(红黑树)的实现方式,即添加到一个有序列表,在O(log n)的复杂度内通过key值找到value,优点是空间要求低,但在时间上不如HashMap。C++中Map的实现就是基于这种方式HashMap是基于HashCode的实现方式,在查找上要比TreeMap速度快(o(1)),添加时也没有任何顺序,但空间复杂度高。C++ unordered_Map就是基于该种方式。
hashmap原理:1. 哈希表的优点在于把数据存储和消耗的时间大大降低,与之对应的代价是空间的消耗。 2. 基本原理:使用一个下标比较大的数组来存储元素,设计一个哈希函数(散列函数),使得每个元素值都和下标对应。但是这样并不能保证每个元素(value)和关键字(key)一一对应,可能会出现对不同的元素计算出相同的函数值,这样就导致了冲突。
hash表解决冲突的方式: 1.线性探测法:在发生冲突时从发生冲突的位置向下一个单元移动,直到下以恶搞单元为空时将元素插入。 2. 平方探测法:若当前key与原来key产生相同的哈希地址,则当前key存在该地址后偏移量为(1,2,3…)的二次方地址处
key1:hash(key)+0
key2:hash(key)+1^2
key3:hash(key)+2^2
3.再哈希法: 同时构造多个哈希函数,Hi=RHi(key) i=1,2,3,k….当H1=RH1(key)发生冲突时,再用H2=RH2(key)计算,直到不产生冲突。 4. 链地址法:将哈希值相同的元素构成一个同义词的单链表,并将单链表的头指针放在哈希表的单元格中,查找,插入和删除都在链表中进行。适用于进程进行删除和插入的情况。
算法概观
下面简述部分STL中的一些算法。
质变算法:指运算过程中会改变区间内元素内容,比如排序,删除等。
非质变算法:不改变操作对象的值,比如查找,计数等。
泛化算法
find()
template<class Iterator,class T>
Iterator find(Iterator begin,Iterator end,const&value){
while(begin!=end && *begin!=value)
begin++;
return begin;
}equal() //如果两个序列在 [first,last) 间相等, 返回true,如果第二个序列元素较多,多出的元素不考虑。如果第二个序列元素比第一个序列元素少,会出错,因此开始前需要先比较元素个数。
template<class InputIterator1,class InputIterator2,class BinaryPredicate>
inline bool equal(InputIterator first1,InputIterator last1,InputIterator first2,inputIterator last2,BinaryPredicate binary_pred){
for(;first1!=last1;++first1,++first2)
if(!binary_pred(*first1,*first2))
return false;
return true;
}fill(first,last,value) //[first,last)内的所有元素都填入新值
fill_n(first,last,n,value)//[first,last) 内n个元素填入新值
lexicographical_compare()//按序对两个序列的元素进行比较可能结果
- 如果第一个序列结果比较小,返回true
- 如果到达last1没有到达last2,返回true,如果到达last2,没有到达last1返回false
- 如果同时到达last1,last2返回false
max()/min() //比较两个元素大小 返回较大/较小值
template<class T>
inline const T&max(const T&a,const T&b){
return a>b?a:b;
}note: 8.23更新
copy_backward(beg, end, dest); // 从输入范围中拷贝元素到指定目的位置。如果范围为空,则返回值为 dest;否则,返回值表示从 *beg 中拷贝或移动的元素。
set相关算法
STL中set相关算法包括并集,交集,差集,对称差集
set_union(first1,last1,first2,last2) //返回[first1,last1)和[first2,last2)之间的所有元素,注意此处set为有序序列(底层是set),序列中允许出现重复数据。
set_intersection()//求存在于[first1,last1)且存在于[first2,last2)之间的所有元素。注意此处set为有序序列(底层是set),序列中允许出现重复数据。
set_difference() //求存在于[first1,last1)且不存在于[first2,last2)之间的所有元素,注意此处set为有序序列(底层是set),序列中允许出现重复数据。
set_symmetric_difference //对称差集,求存在于[first1,last1)且不存在于[first2,last2)之间的所有元素,且存在于[first2,last2)且不存在于[first1,last1)之间的所有元素.注意此处set为有序序列(底层是set),序列中允许出现重复数据。
其他算法
count(first,last,value) // 计算[first,last)间值为value的个数
count_if(first,last,pred) //计算[first,last)间满足条件pre的元素个数
find(first,last,value) //找出区间内第一个满足条件为value的元素
find_if(first,last,pred) //找不区间内第一个满足条件pred的元素
find_end(first1,last1,first2,last2) //在序列一的区间内找序列二最后出现的位置,找不到返回last1
find_first_of(first1,last1,first2,last2) //查找[first2,last2) 第一次出现在[first1,last1)的位置,如果找不到,返回last1;
for_each(first,last,function f) //对输入序列中的每个元素应用可调用对象f,f的返回值被忽略.
generate(first,last,Gen) //将反函数Gen的运算结果填写在[first,last)区间
includes(firsst1,last1,first2,last2) //判断序列[first2,last2)是否包含于[first1,last1),返回bool值, 两个序列都是有序的
merge(fis1,las1,fis2,las2,dst) // 将两个有序序列合并成一个有序序列,填入dst中。
partition(first,last,pred) //在区间内,满足条件的元素放在前面,不满足条件的元素放在后面,返回第一个迭代器。
remove(first,last,value) //移出区间中等于value的元素,并未真正移出,而是将不等于value的元素赋值给first开始的区间
remove(first,last,output,value) //将区间中不等于value的元素移动到output区间内。
replace(first,last,old,new) //将区间内的old都已new代替
replace_if(first,last,pred,new) //区间内满足条件pred的值都会被new代替
reverse(first,last) //将元素在原容器中颠倒重拍
reverse_cpoy(first,last,out) //将元素重排,但是输出到out
rotate(first,mid,last) //将[first,mid)放到原区间后面,[mid,last)放到前面
unique(first,last) //移出区间内相邻的相同元素,保留一个
lower_bound(beg, end, val);// 返回一个非递减序列 [beg, end) 中的第一个大于等于值 val 的位置的迭代器,不存在则返回 end
lower_bound(beg, end, val, comp); // 返回一个非递减序列 [beg, end) 中的第一个大于等于值 val 的位置的迭代器,不存在则返回 end
upper_bound(beg, end, val); // 返回一个非递减序列 [beg, end) 中第一个大于 val 的位置的迭代器,不存在则返回 end
upper_bound(beg, end, val, comp); // 返回一个非递减序列 [beg, end) 中第一个大于 val 的位置的迭代器,不存在则返回 end
binary_search(beg, end, val); // 返回一个 bool 值,指出序列中是否包含等于 val 的元素。对于两个值 x 和 y,当 x 不小于 y 且 y 也不小于 x 时,认为它们相等。