问题
Akari 问题,又名 Beleuchtung 或 Light up 问题,是由日本一家游戏公司于 2001 年创作的一种二进制式逻辑解谜游戏,在当时的环境中引起一阵狂潮。
接下来我们将通过回溯法来对 Akari 问题进行求解,并充分利用计算机并行技术的优势对算法进行改进,从而更迅速的求解问题。
ps: https://www.puzzle-light-up.com/ 是一个在线解决light up谜题的网站。
这道题目是我们暑期作业的一道比较有意思的题目,类型类似于经典的扫雷游戏,游戏规则如下:
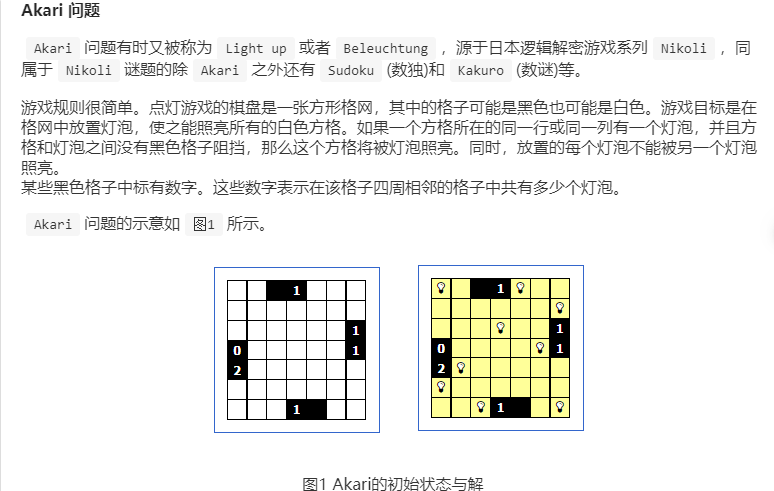
在编程时的要求是:
- 原始迷宫中包括两种格子,白色格子用来放灯泡或者被点亮。
- 黑色格子中根据数字不同可以在周围放不同数目的灯泡,数字为4,只有一种放法。
- 如果数字为3则最多有4中方式
- 如果数字是2,则最多有6中放置方式
- 如果数字是1,则最多有4种放置方式
- 如果数字是0,则不可以放置灯泡
- 如果没有数字,则周围可以放任多的数字
- 在所有数字周围都放置了灯泡后,剩余没有点亮的位置可以放灯泡。
解题思路
要完成这个题目,需要知道的是在我们的题目中是一定有解的,我们的目标是找到其中一个解即可。
还有一点是这个题目比较复杂,建议想要了解的话先去题目前面介绍的网址处试玩游戏。
接下来讲一下我的思路,其实思路大体上都是一致的,只不过根据解答的时候使用不同的数据结构会有不一样的效果。
- 首先明确我们需要解决的问题分为三大步,第一步是点亮数字为4周围的灯,接下来有两种方式,一种是直接进行回溯法,另一种方式是继续解决其中数字与周围空白相同的相同的位置,将其点亮。然后进行回溯。(其实第二种 也可以归为第一种,只是处理方式更符合四位而已)
- 第二步就是上面说的回溯,回溯的方式可以参考网上的很多博客,回溯的目的就是找到一个可以完全符合题目要求的解。
- 完成上面两步后,需要完成的下一步是如果此时还有一些位置没有点亮,则需要采用第二次的回溯方式,回溯的目的是得到最终解。
解答过程
先说第一种先解决所有确定位置的方法,主要思路是使用一个数组保存原始数组,然后开始变换,循环的终止条件是当两个数组完全相同,此时所有确定位置已经确定了,此处我们使用vector完成,接下来是回溯,其中的难点在于如何保证可以实现数字不为4和0时,处理多种情况。这里使用的思路是使用多层循环,然后使用两个数组实现四个方向的变换,

最后也是记录下没有被点亮的灯,然后再次使用回溯将剩余部分点亮。
具体可以参考github中的代码,test.cpp https://github.com/SJ110/some_course_of_three_second/tree/master/%E5%B9%B6%E8%A1%8C%E5%A4%A7%E4%BD%9C%E4%B8%9A
然后是第二种思路,第二种思路就比较厉害了,是当时班上一个大佬给出的思路,他直接跳出了当时题目给出的模板,这个是我一开始没有想到的,然后是对原始迷宫,他的思路是将迷宫带有数字的块使用链表(数组也可以)保存起来,首先保存4和0,其次是1,2,3的块,然后第一遍循环将4和0周围点亮,接下来是回溯法,首先使用一个数组保存现在的迷宫,进行下一次循环,使用case不同的项,然后使用列举的方式列举处每一种情况,如果是3,最多有4种情况,每一遍处理后我们判断当前的迷宫是否符合题意,如果不符合,则退回上一次保存的数组,如果满足题意,则更新保存的数组。进行下一次回溯直到链表尾部。
完成这一步后使用相同的思路解决没有被点亮的空白区域。
源码参考m_akari.cpp
https://github.com/SJ110/some_course_of_three_second/tree/master/%E5%B9%B6%E8%A1%8C%E5%A4%A7%E4%BD%9C%E4%B8%9A
这个题目其实很有意思,一开始是比较迷惑的,而且玩着那个游戏也比较有意思,但是慢慢研究后有了思路就慢慢清楚起来,其中的难点就是我上面说到的几点。但是不同的解决思路却是导致完全不同的代码量,这里我也意识到大佬写的代码真的很优雅。有时候多看下别人的代码还是很有收获的。
总结
然后这篇blog来的比较晚,主要是这十几天来都去玩去了,中间做的事比较少,也不想直接更新一些自己的琐事,不过接下来到开学尽量多更新一些东西吧。下一次更新一下前段时间的一道leetcode题目吧。