题目
题目如图
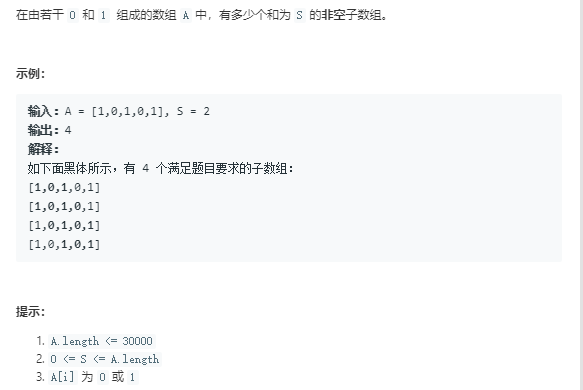
这里题意我个人认为不太清楚,这里解释一下:大致意思是从一个只由0和1组成的数组中找出所有连续数字之和为S的子数组。注意此处S可以为0。当然最后只需要统计总数。
思路
基本思路,超出时间限制
所以思路也比较清晰:大致就是遍历整个数组,然后得到最后的结果。既然要遍历数组那就需要索引,然后再从题目得知每个解都是一个数组,所以可以考虑双指针。基本思路确定后我们考虑下如何遍历整个数组。
一个比较直接的思路是顺序扫描数组每个元素,和为S时对这一段进行处理。
处理的方式也有很多种,以left right作为左右索引为例,只要right指向的元素为0,则结果+1,直到指向的元素为1. 然后left+1,right=left,再从此处再一次遍历直到和为S, 退出循环的条件是right<A.size()。这个思路带来的结果是会在后面几个样例超时。但此处还是给出具体代码。还需要指出的是0是一个特殊情况,我这里的处理是将0分开处理了。
超时代码
class Solution {
public:
int numSubarraysWithSum(vector<int>& A, int S) {
int left=0;
int right=0;
int ret=0;
if(A.empty()) return 0;
int tmp=0;
// S=0 单独处理
if(S==0){
while(right<A.size()){
if(A[right]==0){
ret++;
right++;
while(right<A.size() && A[right]==0){
ret++;
right++;
}
left++;
right=left;
}else {
right++;
left=right;
}
}
return ret;
}
while(right<A.size()){
tmp=tmp+A[right];
if(tmp==S){
ret++;
left++;
right++;
while(right<A.size() && A[right]==0){
ret++;
right++;
}
tmp=0;
right=left;
}
else right++;
}
return ret;
}
};上述代码的时间复杂度o(n^2),空间复杂度o(1)常数级别。
优化思路
上面的代码可以很容易的看出,其实每次在S==temp中都会使right倒退很多步,导致进行了很多重复的计算,所以考虑从这里优化。
从另一个角度来看,数组的每个元素都是0 或者1,因此我的思路是存储所有的1的下标,然后采用采用窗口滑动的形式从左到右依次处理每个窗口。
这里再提一点,就是计算每个窗口解的个数时我是计算left左边和right右边的0的个数得到的。 因为是窗口滑动,所以就不需要太多的重复计算,每个窗口大小即为S.
AC代码
class Solution {
public:
int numSubarraysWithSum(vector<int>& A, int S) {
int left=0;
int right=0;
int ret=0;
if(A.empty()) return 0;
// S=0 单独处理
if(S==0){
while(right<A.size()){
if(A[right]==0){
ret++;
right++;
while(right<A.size() && A[right]==0){
ret++;
right++;
}
left++;
right=left;
}else {
right++;
left=right;
}
}
return ret;
}
// while(right<A.size()){
// int tmp=0;
// while(right<A.size() && tmp!=S){
// tmp=tmp+A[right];
// right++;
// }
// if(tmp!=S) break;
// ret++;
// left++;
// while(right<A.size() && A[right]==0){
// ret++;
// right++;
// }
// right=left;
// }
int tmp=0;
vector<int> help;
for(int i=0;i<A.size();i++){
if(A[i]==1)
help.push_back(i);
}
if(S>help.size()) return 0;
int i=0;
while(i+S<=help.size()){
left=help[i];
right=help[S+i-1];
int countleft=0;
left--;
while(left>=0 && A[left]==0){
countleft++;
left--;
}
int countright=0;
right++;
while(right<A.size() && A[right]==0){
countright++;
right++;
}
ret=ret+(countleft+1)*(countright+1);
i++;
}
return ret;
}
};复杂度分析: 时间复杂度 o(n^2) 空间复杂度 o(n); 表面上看复杂度好像更高了,但是循环条件有所优化,内部第二层循环也没有过多重复,内部二层循环消耗不高,所以最后可以access。
本题评论区有人做出了 o(n)时间复杂度,o(1)空间复杂度。可以去参考一下。
最后贴一张ac的截图