题意
给定一棵二叉树,返回他的前序遍历
解析
题意本身比较简单,但是本题要求不使用递归思想来实现,如果不需要查看此处的递归思路,直接查看非递归思路。此处可以先复习下树的遍历方式。对于一棵树来讲:
递归思路
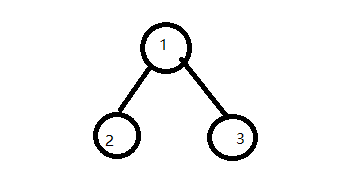
前序遍历: 根,左子树,右子树
中序遍历:左子树,根,右子树
后序遍历: 左子树,右子树,根
对于上面这棵树 前序 123 中序 213 后续 231
由于树本身的特性,在进行递归算法时我们要抓住得一点就是树得任何一个节点及其子树单独拿出来也是一棵树。所以前序遍历将原本得树看成三棵子树,然后每棵子树也可进行递归。
代码如下
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
private:
vector<int> ret;
public:
vector<int> preorderTraversal(TreeNode* root) {
preorderhelp(root);
return ret;
}
private:
void preorderhelp(TreeNode* root){
if(root==NULL) return;
ret.push_back(root->val);
preorderhelp(root->left);
preorderhelp(root->right);
return;
}
};递归思想作用在函数preorderhelp中;
注意其中三行
ret.push_back(root->val); //根
preorderhelp(root->left); //左子树
preorderhelp(root->right); //右子树也就是说树的递归遍历实际就是这三行代码。但是关键还是多去看看数据结构,重在理解。
非递归思路
要完成前序遍历,首先我们明确一点,在前序遍历中,树是从最左边得一层开始遍历得,换句话说我们对树进行深度优先搜索,搜索到树的最左边的节点即是树的部分前序遍历结果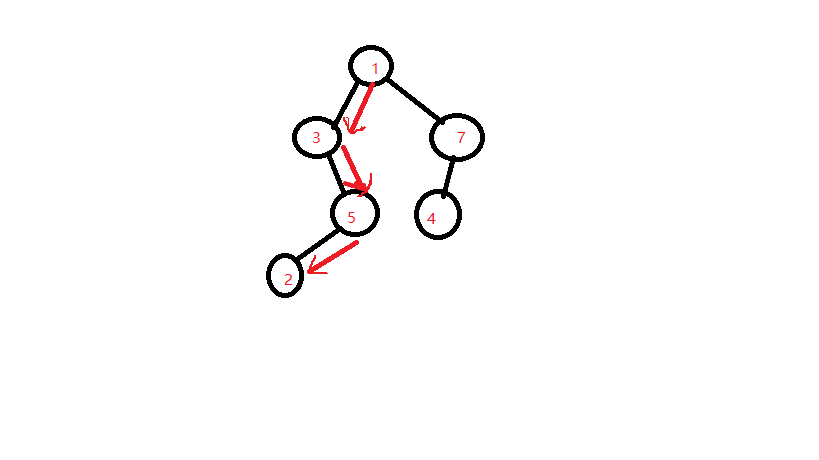
如图所示,我们可以对树进行深度优先搜索得到树的部分前序遍历,而为了得到整棵树的遍历,我们采用queue或者stack存放这些节点,每次pop一个节点,然后取当前节点的栈顶/队尾节点,如果当前节点的右孩子存在且不等于pop出来的节点,就说明当前节点有右子树,我们接采用同样深度遍历的方式去遍历这棵子树,那最后是否遍历完成,取决于queue或者stack是否empty
while(root){
ret.push_back(root->val);
help.push_back(root);
if(root->left) root=root->left;
else root=root->right;
}这是则部分代码最主要的思想。
这个思路其实比较简单,只要理解了了就很容易得到代码,关键在于我们一开始构建的queue/stack是树的部分前序遍历,这保证了这个算法的正确性。以下是代码
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> ret;
if(root==NULL) return ret;
vector<TreeNode*> help;
while(root){
ret.push_back(root->val);
help.push_back(root);
if(root->left) root=root->left;
else root=root->right;
}
cout<<help.size();
while(!help.empty()){
TreeNode*child= help.back();
help.pop_back();
TreeNode* parent=nullptr;
if(!help.empty()){
parent=help.back();
if(parent->right && parent->right!=child){
TreeNode* tmp=parent->right;
cout<<tmp->val<<" ";
while(tmp){
ret.push_back(tmp->val);
help.push_back(tmp);
if(tmp->left){
tmp=tmp->left;
}else {
// help.push_back(tmp->right);
tmp=tmp->right;
}
}
}
}
}
return ret;
}
};然后这是非递归思路得通过图:
好的,关于这道题就说这些了,在我看来,树和图的数据结构还是得多加练习,它不像数组和链表一样便于接受,树和图其实比较抽象,多加练习即可得出套路所在。
这是我的第一篇博客,写的不好,还请多多见谅。谢谢。